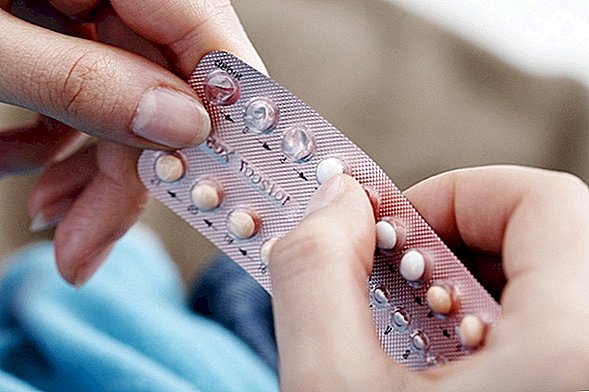
Bildtext: Vy över månen vid perigee och apogee
Som lärare är jag alltid ute efter labb med enkla inställningar som är lämpliga för elever. Min nuvarande favorit är att hitta ljusets hastighet med choklad.
I ett nytt papper som nyligen laddats upp till arXiv beskriver Kevin Krisciunas från Texas A&M en metod för att bestämma månens orbital excentricitet med ett förvånansvärt lågt fel genom att använda bara en meterpinne, en kartongbit och ett program som är avsett att anpassa kurvor till variabla stjärnor.
Denna metod använder sig av det faktum att excentriciteten kan bestämmas utifrån förhållandet mellan medelvinkelstorleken för ett objekt och hälften av dess amplitud. Således är huvudmålet att mäta dessa två kvantiteter.
Kevins strategi för att göra detta är att använda ett kartongsiktningshål som kan glida längs en meterpinne. Genom att kika igenom hålet på månen och skjuta kortet fram och tillbaka tills hålets vinklade storlek bara överlappar månen. Därifrån ger hålets diameter dividerat med avståndet nerför mätpinnen vinkelstorleken tack vare den lilla vinkelformeln (? = D / D i radianer om D >> d).
För att förhindra systematiska fel vid felbedömning när kortet skjuts fram tills hålets storlek matchar månen, är det bäst att också närma sig det från den andra riktningen; Kommer in från bortre änden av meterpinnen. Detta skulle hjälpa till att minska fel och i Kevins försök fann han att han hade en typisk spridning på ± 4 mm när han gjorde det.
Vid denna tidpunkt finns det ännu ett systematiskt fel som måste beaktas: Eleven har en ändlig storlek som är jämförbar med synhålet. Detta kommer att göra att den faktiska vinkelstorleken underskattas. Som sådan är en korrigeringsfaktor nödvändig.
För att härleda denna korrigeringsfaktor placerade Kevin en 91 mm skiva på ett avstånd av 10 meter (detta skulle producera en skiva med samma vinkelstorlek som månen när man tittar från det avståndet). För att producera den bästa matchen, kartongmallen med synhålet skall måste placeras på 681,3 mm på mätpinnen, men på grund av elevernas systematiska fel fann Kevin att det behövde placeras på 821 mm. Förhållandet mellan den observerade placeringen och rätt placering gav korrektionsfaktorn Kevin använde (1.205). Detta måste kalibreras för varje enskild person och skulle också bero på mängden ljus under observationstiden eftersom detta också påverkar pupillens diameter. Att anta en enda korrigeringsfaktor ger dock tillfredsställande resultat.
Detta möjliggör korrekt tagna data som sedan kan användas för att bestämma de nödvändiga mängderna (medelvinkelstorleken och 1/2 amplituden). För att bestämma dessa använde Kevin ett program som kallas PERDET som är utformat för att anpassa sinusformade kurvor till svängningar i variabla stjärnor. Vilket program som kan passa sådana kurvor till datapunkter med hjälp av en?2 passform eller en Fourier-analys skulle vara lämplig för detta ändamål.
Från sådana program när medelvinkelstorleken och halvamplituden har bestämts ger deras förhållande excentriciteten. För Kevins experiment fann han ett värde av 0,039 ± 0,006. Dessutom var perioden han bestämde från perigee till perigee 27,24 ± 0,29 dagar, vilket är i utmärkt överensstämmelse med det accepterade värdet på 27,55 dagar.